In-Place Quicksort
25 Apr 2013Quicksort has a space complexity of O(log(n)) (pessimistic case being O(n)). It follows from the fact that it is recursive and stack has to be kept. For some recursive algorithms it can be avoided by using tail calls, but quicksort requires two recursive calls making this impossible.
It is, however, possible to implement it in-place (i.e. with constant space complexity O(1)) using a nifty trick.
First let's figure out where the problem is. After picking a pivot and reordering elements there are two subtables left to sort. Assuming proceeding to left one position of the right subtable has to be remembered (preferably on a stack) so that the algorithm can come back to it later. But there's a way not to do that.
The trick is to find maximum of the right subtable an put it at the beginning. Now:
- It doesn't mess up time complexity. The subtable will have to be walked through anyway during reordering later on.
- It makes possible to find the right end. After the right subtable comes either an end of table or a pivot, which is guaranteed to be larger than any element to it's left.
- Finding the beginning of right subtable is straightforward: it the second element after the end of the left subtable.
This is a schematics of the algorithm:
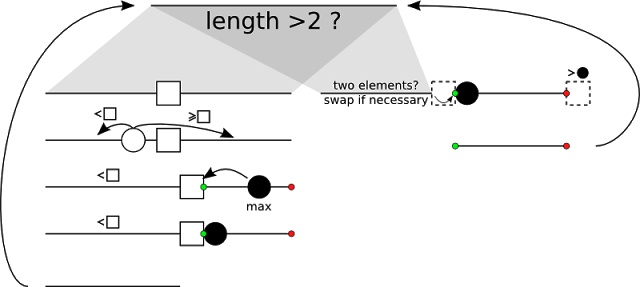
Notice that in the left branch (length > 2) we proceed with left subtable so we have to be able to locate boundaries of right subtable (represented by green and red dot) later on. When we "hit the bottom" and subtable is only two elements long we have to swap them if necessary and return to the last right subtable left behind. The green beginning is the second element after the end of current subtable - we also know it's the largest element in subtable we're looking for. Thus to find the red end we find the last element not greater than the black circle maximum at the beginning.
While this trick technically doesn't change time complexity this type of quicksort takes longer time because of all the maximum searching. But you can sort with it arbitrarily big table using just a few bytes of memory.
It can be easily implemented in a while loop remembering only two pointers to mark boundaries of current list.